Шкільна математична формула для розрахунку виграшу в лотереї показує стільки нулів для шансу виграти, що одразу стає зрозуміло – це даремне витрачання грошей. Однак нулі можуть бути недостатньо наочними для людей, які вірять, що можуть виграти. Можливо, сайт Lottery Every Second (розіграш лотереї щосекунди) допоможе зрозуміти, що зробити ставку в лотереї означає просто віддати свої гроші організаторам лотереї. Девіз сайту: “Навіщо чекати тиждень, щоб розчаруватися, якщо ви можете отримувати розчарування щосекунди?” (лотереї зазвичай проводять розіграші раз в тиждень, щоб мати час подражнити людей багатомільйонним джек-потом).
«Lottery Every Second» (lotteryeverysecond.lffl.me) є проєктом, який, відповідно до своєї назви, моделює гру в лотерею щосекунди. Точніше кажучи, він одночасно імітує участь одразу у двох лотереях кожної секунди: Powerball, одній з найпопулярніших лотерей у Сполучених Штатах Америки, та EuroJackpot, подібній за принципом грі, що проводиться в багатьох європейських країнах.
Обидві лотереї працюють за загалом схожою логікою. У Powerball необхідно вибрати п’ять чисел у діапазоні від 1 до 69 та шосте число в діапазоні від 1 до 26. Для виграшу джекпоту всі шість вибраних чисел мають повністю збігтися з числами, випадково визначеними під час конкретного розіграшу. У EuroJackpot правила дещо інші: гравець обирає п’ять чисел від 1 до 50 та ще два додаткові числа від 1 до 12. Як і у випадку з Powerball, для виграшу джекпоту необхідний повний збіг усіх чисел.
Імовірності виграшу нескладно обчислити самостійно. Для Powerball імовірність правильного вибору кожного з перших п’яти чисел становить одну з 69, а для шостого числа одну з 26. Щоб отримати загальну імовірність виграшу джекпоту, ці значення необхідно перемножити. У результаті виходить імовірність один до 292 201 338. У випадку EuroJackpot шанси є дещо кращими і становлять приблизно один до 139 838 160.
На перший погляд ці цифри можуть здатися не надто загрозливими. Проте, як зазначає пояснювальний текст проєкту «Lottery Every Second», такі числа настільки великі, що людський мозок фактично не здатен інтуїтивно осмислити їхній реальний масштаб. Саме цю проблему і намагається продемонструвати сайт, показуючи, що означають ці імовірності на практиці. Згідно з наведеними розрахунками, у середньому необхідно безперервно спостерігати за симуляцією, яка відбувається щосекунди, трохи більше двох років, щоб побачити один виграш джекпоту EuroJackpot, і приблизно чотири з половиною роки, щоб побачити виграш джекпоту Powerball. При цьому наголошується, що йдеться саме про один розіграш кожної секунди. Якщо ж купувати один лотерейний квиток на тиждень, то для досягнення приблизно 50-відсоткової ймовірності виграти хоча б один раз у Powerball знадобилося б грати близько 5,6 мільйона років.
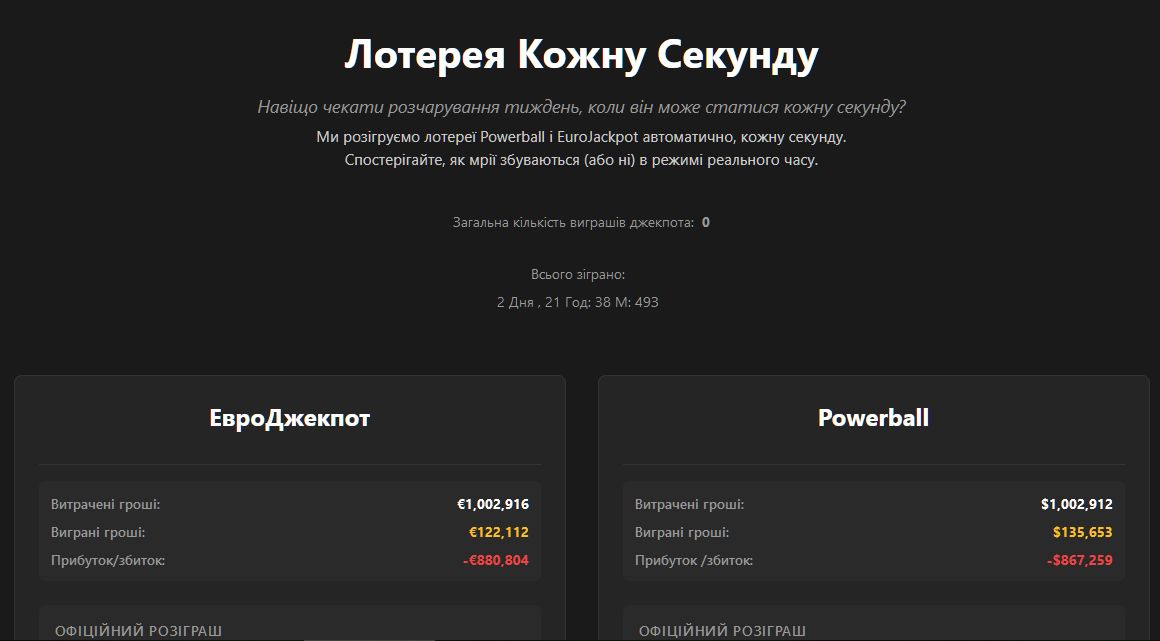
Ще один аспект, який наочно демонструє цей проєкт, полягає в обсягах коштів, що їх отримують організатори таких ігор. Симуляція веде постійний підрахунок виграшів і програшів, і попри те, що EuroJackpot на перший погляд виглядає значно вигіднішим для гравця, в обох випадках загальна сума виплат становить приблизно одну восьму від суми отриманих коштів. Іншими словами, на кожні умовні 100 доларів, які оператор виплачує у вигляді виграшів, він отримує близько 800 доларів. Фактично йдеться про надзвичайно прибуткову модель з мінімальним фінансовим ризиком для організаторів.
Можна сподіватися, що наочне представлення абсурдних за своїм масштабом чисел, які характеризують лотерейні імовірності, змусить частину людей замислитися і відмовитися від регулярного придбання лотерейних квитків. Проте люди не є виключно раціональними істотами. На поведінку впливають надія, імпульсивність і відчай, а також загальна схильність погано оцінювати статистичні ймовірності. Тому навіть якщо участь у Powerball чи подібних лотереях триватиме попри всі ці факти, це залишається особистим вибором. У разі ж несподіваного виграшу варто пам’ятати, що випадкові події не зникають з життя разом із великим чеком, і статистика загалом не стає прихильнішою лише тому, що цього разу пощастило.
Чому купувати лотерейний квиток означає просто віддати свої гроші
Доцільно окремо розглянути математичний апарат, який лежить в основі розрахунку шансів виграшу джекпоту, оскільки саме тут інтуїтивні уявлення людини найчастіше радикально розходяться з реальністю.
Людина купує один лотерейний квиток на тиждень? Вам потрібно було б грати в Powerball приблизно 5,6 мільйона років, щоб мати 50%-ний шанс виграти один раз. Неандертальці вимерли всього 40 000 років тому. Вид людини, до якого належите ви, існує близько 300 000 років. Вам потрібно було б прожити всю історію сучасних людей 18 разів.
У вас більше шансів бути ураженим блискавкою (1 до 15 300), стати кінозіркою (1 до 1 505 000) або отримати флеш-рояль в покері у першій роздачі (1 до 649 740), ніж виграти джекпот у лотерею.
У лотереях типу Powerball або EuroJackpot використовується класична комбінаторна модель, у якій важливим є не порядок вибраних чисел, а лише їхній повний збіг із комбінацією цифр, визначеною під час розіграшу. Це означає, що кожна можлива комбінація чисел є рівноймовірною, а загальна кількість таких комбінацій визначається кількістю способів вибрати задану кількість чисел з певного діапазону без повторень. Для цього використовується формула числа комбінацій, яка в математиці позначається як C(n, k), де n — загальна кількість можливих чисел, а k — кількість чисел, які необхідно вибрати.
У випадку Powerball перша частина білета передбачає вибір п’яти чисел з 69 можливих. Кількість усіх можливих комбінацій для цього вибору дорівнює C(69, 5), що становить 11 238 513 різних варіантів. Друга частина полягає у виборі одного додаткового числа з 26 можливих, що дає ще 26 варіантів. Оскільки ці дві частини є незалежними одна від одної, загальна кількість можливих комбінацій дорівнює добутку цих значень, тобто 11 238 513, помножених на 26. У результаті отримується 292 201 338 унікальних комбінацій, з яких лише одна відповідає джекпоту. Саме звідси походить імовірність виграшу один до 292 201 338.
Аналогічний підхід застосовується і до EuroJackpot. Основна частина гри передбачає вибір п’яти чисел з 50 можливих, що дає C(50, 5) або 2 118 760 комбінацій. Додатково необхідно вибрати два числа з 12 можливих, а кількість таких комбінацій дорівнює C(12, 2), тобто 66. Перемноживши ці значення, отримуємо 139 838 160 можливих комбінацій. Як і у випадку з Powerball, лише одна з них відповідає виграшу джекпоту, що й визначає відповідну імовірність.
Важливо підкреслити, часто люди вважають, ніби шанси виграти накопичуються, якщо грати тривалий час. Але кожен окремий білет має абсолютно однаковий шанс виграшу незалежно від того, скільки білетів було придбано раніше і скільки розіграшів уже відбулося без виграшу. Це означає, що ймовірність не накопичується з часом і не зростає через серії програшів. Кожен розіграш є статистично незалежною подією, а поширене уявлення про те, що виграш «має ось-ось статися», не має жодного математичного підґрунтя.
Для кращого розуміння масштабів цих чисел варто звернути увагу на ще один аспект. Навіть якщо купувати не один, а, наприклад, сто білетів на кожен розіграш, імовірність виграшу джекпоту зросте лише в сто разів, але при настільки великих знаменниках це майже не змінює загальної картини. Замість одного шансу з приблизно 292 мільйонів у випадку Powerball мова йтиме про один шанс з приблизно 2,9 мільйона, що все одно залишається статистично мізерною величиною.
Саме ця непропорційність між інтуїтивним сприйняттям «багатьох спроб» і реальними комбінаторними масштабами робить лотерейні імовірності настільки оманливими для більшості людей.